Decisions are processes that select among options. The goal is thus to produce a final choice based on evaluation criteria. This is a very complex cognitive task and while we often do it unconsciously and very fast, it also is subject to many factors that influence sometimes in a contradictory way the final outcomes. Some aspects of decision theory that warrant an entire field of research are:

• Choice under uncertainty
• Intertemporal choice
• Interrelated decision making, i.e. within a social context (network)
• Social preferences, such as fairness, compassion etc
• Complexity of decision maker (resource/information limitation or bounded rationality)
• Complexity of the system producing the outcomes of decisions

While we know a great deal on many of these, it becomes obvious that the optimal decision is something that is very hard to make. Yet we do them everyday. Economic theory has developed tools that inform decision making based on simplified models of reality and rational reasoning. We can use these to understand when and how they fail.

A typical decision process can involve:

Deciding on a goal, i.e. what is the objective(s) to achieve? What are the constraints? These include knowledge and understanding about the system we are trying to affect. What can we change? Or, what are our options? How do we evaluate, i.e. which criteria is it we are trying to maximize?

As you can see, there are a lot of decisions to make even before one can start making this decision! Also, the process depends largely on the social scale we are looking at, whether it is one person, a group with a shared goal such as in management or if it involves multiple stakeholders or levels of governance. For the latter, all four points can vary among participating groups and there is a social process involved, including deliberation, power relations and social influence. In principle, IF everything is known, an optimal solution can be found.

The production system

As we have seen in the lectures of markets and taxes and subsidies finding an optimal solution is rather easy when everything is known and static, i.e. we find the optimal decision where demand and supply intersect. When a control option is given (taxation/subsidies) we can easily find out how to choose it in order to find the socially desirable outcome. But most systems that provide us with the utility we want are complex adaptive systems and thus non-linear and unpredictable. While there are many aspects that complicate decision making in such systems, we will look at a few particularly important ones here:

• Dynamics, i.e. change
• Risk and uncertainty
• Regime shifts
• Regime shifts and uncertainty

Dynamics

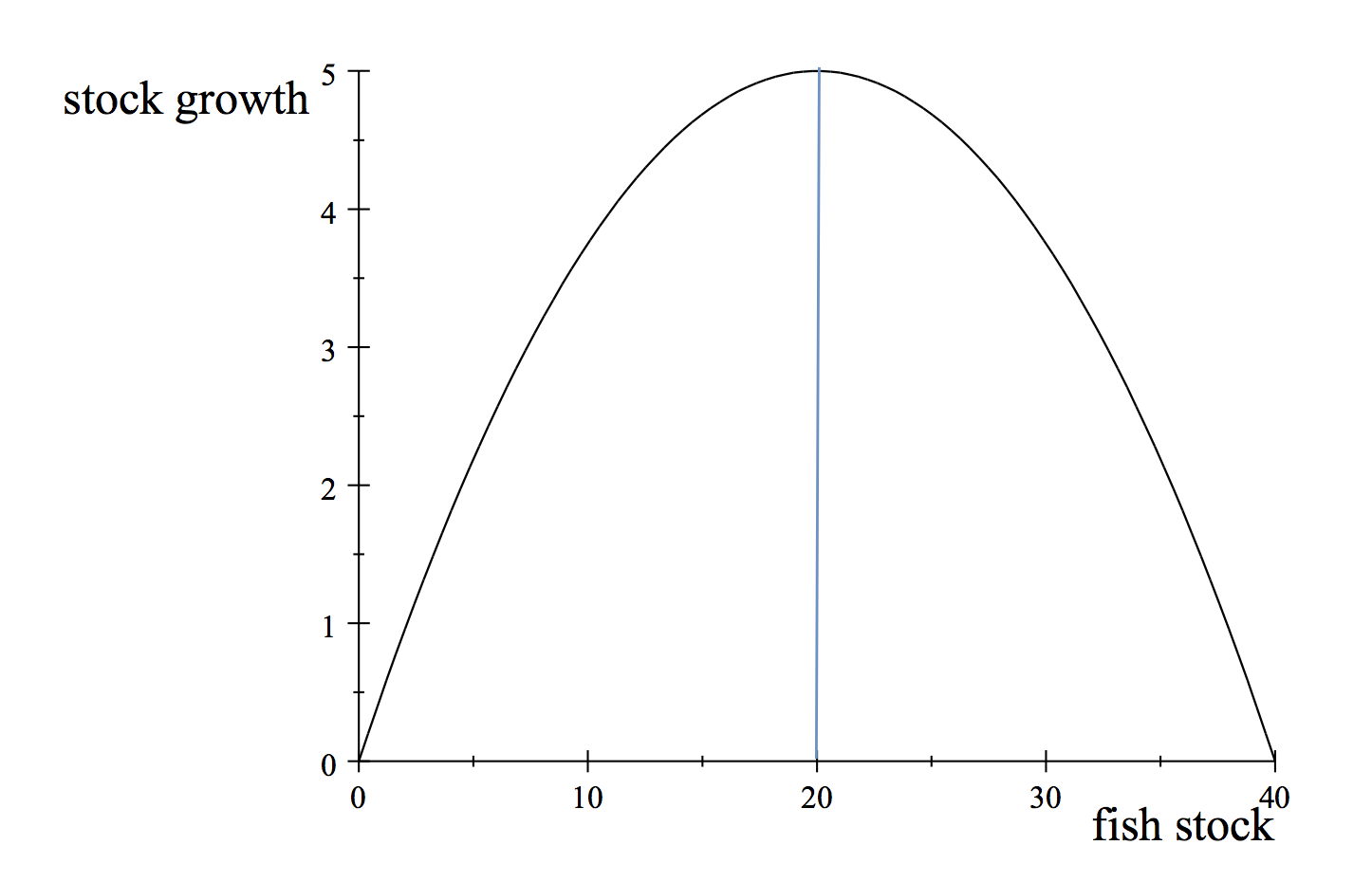
In this figure we show not a static picture of utility of the stock, but how its rate of increase depends on the stock size. From 0-20 stock growth increases because the more fish you have, the more fish are reproduced per year, and are add to the next year’s stock. Between 20-40 growth decreases (but is still positive) due to the fact that food or habitat resources for the fish become limited. Optimally, and ignoring that catching fish has a cost, the optimal catch rate would be 5, because if we catch 5 per year and the stock growth 5 per year we can utilize the maximum sustainable yield of the fish population, i.e. without causing a decrease in the stock size and thus stock regrowth. However, stock size may vary due to many reasons, such as predation from other species or fluctuations in food sources. What would we do if the stock was 10? Economic theory says that for this simplified case, we should do whatever it takes to bring back the stock as fast as possible to 20 and then keep taking 5 each year. This means not harvesting at all until the stock goes above 20 next year and then only take whatever is needed to keep it at 20. But what if the growth rate changes?

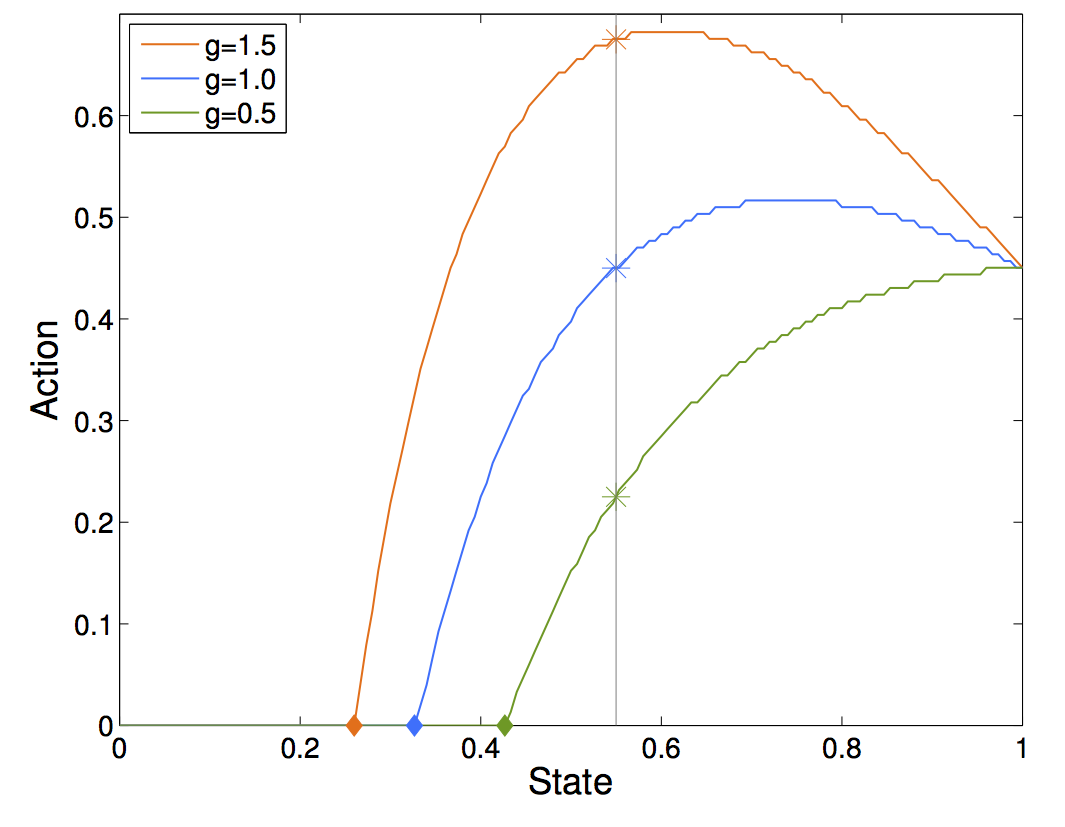
The figure below shows how the optimal action changes depending on different growth rates. If we knew exactly the growth rate and the size of the stock, we could still do optimal decisions. However, any uncertainty causes suboptimal decisions and due to the way the growth depends on last years stock and thus creates a lag between the action and the feedback from the system, any discrepancies can quickly cause cascading dynamics which are hard to control and anticipate. Furthermore, growth rates are even harder to measure than actual fish stock levels.

Dealing with risk and uncertainty

One particular type of uncertainty is when we don’t know what will happen, but we have a good idea about the probabilities. For example, as a farmer in the sub-saharan region, one is faced with a probability of low rainfall any year. But over time (and ignoring climate change trends) the risk of a dry year can be estimated. So, should one plant a high value crop that is drought sensitive or a low value crop that can tolerate drought? You can imagine that this decision depends on your alternatives. If you have an alternative income which you can use to buy food from local markets, then the first option might seem sensible. If a successful crop is the only food you will have for your family, then the second option is the most sensible. What we describe here are different risk aversions. Let’s say that the utility from growing a crop is given probability p of no drought.

U=p * (normal crop yield) + (1-p) * (crop yield with drought)

If we knew the probability of drought (say 20%) and the yields of two different crop types under [normal/drought] to be for drought resistant type [10/5] and drought sensitive type [20/0] we could calculate the expected yield as 9 for the drought tolerant type and 16 for the drought sensitive type. If you don’t care about risk, then the second option is clearly better. But if it is more important to get any crop than maximum crop your strategy would be different. This has to do with risk aversion.

Uncertainty without knowing probabilities

If you cannot estimate probabilities, for example, through past experiences, but there are a couple of other strategies one can apply. We will only list two strategies here, to give you a flavor of how to deal with unknowns. There are many more strategies that involve using more or less information about the system.

Maximin-rule

Select the strategy with the least worst outcome. The decision maker selects the strategy that maximizes the minimum possible payoff. This strategy has the advantage that it avoids the worst possible outcomes but it ignores lots of information which can lead to strange decisions. For example, if one strategy is marginally better in terms of worst outcomes but substantially worse in terms of other outcomes it would be selected although in most state of nature it would be a bad choice. It is a very cautious strategy.

Maximax-rule

Select the strategy with the best of the best outcome. The decision maker selects the strategy that maximizes the maximum possible payoff. This is a very adventurous strategy that ignores again lots of information. It would select a strategy that does marginally better for the best outcomes and substantially worse for the other outcomes even though common sense would typically be in favor of such strategy

Precautionary principle

The precautionary principle is a presumption against projects that could have serious irreversible consequences, such as ones that are often induced by regime shifts. It puts the burden of proof on project proponents to show that their project will not have serious irreversible consequences. Economic theory has extensively discussed whether precaution can be an optimal behavior or not. How does the threat of a potential regime shift affect optimal management? Should it lead to more or less precautionary behavior compared with a case with no regime shift? (Polasky et al 2011). The dilemma is that there is typically a trade-off between precaution and efficiency

• On one hand we must be careful not to end up in a really nasty situation (precautionary principle)
• On the other hand staying too far away from a possible regime shift can result in lost opportunities and decreased welfare (efficiency argument). Postponing actions implies trade-off between learning first and acting first (option value)

Polasky et al. (2011) shows that two factors that influence the answer to this question are whether the manager’s actions actually can influence the probability that the shift occurs and whether the regime shift leads to a total collapse of the stock or if it only changes the renewal dynamics of the stock.

Firstly, if the manager can actually influence the probability that the shift occurs, it seems reasonable that the manager accounts for this in their decisions and tends to behave more precautionary. In contrast, if a manager does not influence the probability of a shift, a precautionary behavior will then not lead to any potential gains and is not motivated.

The second aspect is the question of how dramatic the regime shift is. If there is a risk of an irreversible fish stock collapse, there is some rational in trying to exploit the stock as much as possible before it disappears. Hence it also matters whether the regime shift leads to an irreversible collapse of a stock for example or rather changes the dynamics of resource renewal.

Contributors

Adapted from Anne-Sophie Crepin by Jon Norberg